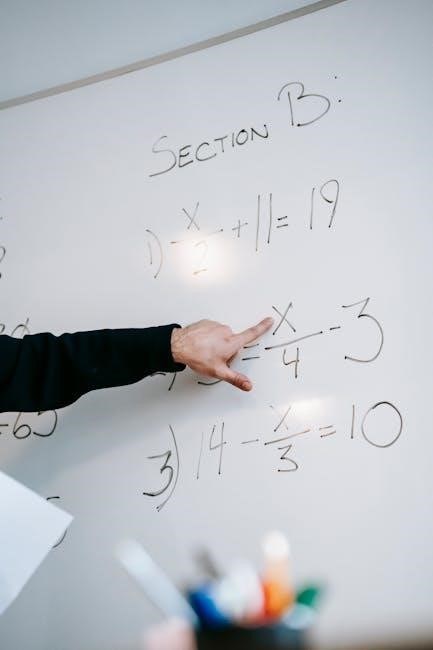Two-step equations involve solving for a variable using two operations, such as multiplication and addition. They are fundamental in algebra, enhancing problem-solving skills and logical thinking. For example, solving 3x + 6 = 12 requires reversing operations. Free PDF worksheets are available for practice, covering various difficulty levels and real-world applications.
1.1 What Are Two-Step Equations?
A two-step equation is a mathematical equation that requires two operations to solve for the unknown variable. These equations typically involve a combination of multiplication, division, addition, or subtraction. For example, an equation like 3x + 6 = 12 requires first subtracting 6 from both sides and then dividing by 3 to find the value of x. Two-step equations are fundamental in algebra, as they build upon basic problem-solving skills and introduce students to more complex algebraic manipulations. They are widely used in various math problems, including word problems and real-world applications. Worksheets and PDF resources are available online to practice solving two-step equations, catering to different skill levels and learning needs.
1.2 Importance of Two-Step Equations in Mathematics
Two-step equations are essential in mathematics as they build foundational algebraic skills, enabling students to solve more complex problems. They enhance critical thinking and problem-solving abilities, which are vital in various STEM fields. Mastering two-step equations prepares learners for advanced algebra, such as quadratic equations and systems of equations. These equations also appear in real-world applications, like calculating distances, budgeting, and scientific formulas. Solving them improves logical reasoning and step-by-step analytical thinking. Additionally, two-step equations are a stepping stone for understanding more intricate mathematical concepts, making them a cornerstone of algebraic education. Free PDF worksheets and online resources provide ample opportunities for practice, ensuring proficiency in this fundamental area of mathematics.

Understanding the Basics of Two-Step Equations
Two-step equations involve solving for a variable using two operations, typically combining like terms and then performing multiplication or division. Mastering these basics is crucial for more complex algebraic manipulation and problem-solving in mathematics. They build upon fundamental arithmetic skills, emphasizing the importance of the order of operations and their reversal in solving equations. Understanding these principles is vital for accurately isolating variables and finding solutions, making them a cornerstone of algebraic problem-solving. Regular practice with worksheets and online tools can enhance proficiency in this area, ensuring a strong foundation for advanced mathematical concepts.
2.1 Definition and Examples
A two-step equation is an algebraic equation requiring two operations to solve for the variable. It involves combining like terms and applying the reverse order of operations. For example, in the equation 3x + 6 = 12, the first step is subtracting 6 from both sides, and the second step is dividing by 3 to find x = 2. Another example is 4y ౼ 8 = 16, where adding 8 to both sides is the first step, and dividing by 4 yields y = 6. These equations are fundamental in algebra, teaching students to methodically isolate variables. Mastering these examples builds a strong foundation for solving more complex equations in mathematics.
2.2 Key Operations Involved in Solving Two-Step Equations
Solving two-step equations involves a combination of inverse operations to isolate the variable. The primary operations include addition, subtraction, multiplication, and division. The order of operations is reversed, meaning multiplication or division is addressed before addition or subtraction. For instance, in an equation like 2x + 4 = 10, subtraction is performed first to eliminate the constant term, followed by division to solve for x. Combining like terms is another critical operation, simplifying the equation before applying inverse operations. Understanding these operations is essential for systematically solving two-step equations and ensuring accuracy in the final solution. Practice reinforces the ability to apply these steps effectively.

Step-by-Step Guide to Solving Two-Step Equations
A step-by-step approach ensures clarity and accuracy. Begin by simplifying both sides, then apply inverse operations to isolate the variable. This systematic method guarantees a solution.
3.1 Identifying the Operations to Perform
Identifying the operations to perform is the first step in solving two-step equations. Examine the equation to determine the order of operations applied to the variable. Common operations include multiplication, division, addition, and subtraction. Look for constants being added or subtracted and coefficients multiplying or dividing the variable. For example, in the equation 3x + 5 = 14, multiplication and addition are applied. Always identify these operations to apply the correct inverse steps later. This step ensures clarity and sets the foundation for solving the equation accurately. Practicing this skill helps in breaking down complex equations into manageable parts.
3.2 Applying the Reverse Order of Operations
After identifying the operations, the next step is to apply them in reverse order. This means performing the inverse operations to isolate the variable. For example, if the equation involves multiplication and then addition, you would first subtract to undo the addition and then divide to undo the multiplication. This systematic approach ensures that each operation is reversed correctly, leading to the accurate solution of the equation. Always remember to apply these operations to both sides of the equation to maintain balance and equality. This methodical process helps in simplifying the equation step by step, ultimately revealing the value of the variable. Consistent practice reinforces this crucial skill in solving two-step equations effectively.
3.3 Simplifying Both Sides of the Equation
Simplifying both sides of the equation is essential to isolate the variable effectively. Start by combining like terms on each side to reduce complexity. For instance, if the equation has multiple constants or similar variables, combine them using addition, subtraction, or multiplication. Ensure that both sides remain balanced by performing the same operation on each. Simplifying step by step prevents errors and makes the equation easier to solve. Always check for any remaining operations that can be combined or eliminated. This process not only clarifies the equation but also prepares it for the final steps of solving. Regular practice helps in mastering this critical step for accurate solutions in two-step equations.

Practicing with Examples
Practicing with various examples is crucial for mastering two-step equations. Solve equations involving multiplication, division, addition, and subtraction to build confidence and improve problem-solving skills effectively.
4.1 Solving Equations with Multiplication and Division
Mastering equations with multiplication and division involves isolating the variable through inverse operations. Start by identifying whether the variable is multiplied or divided by a number. For equations like (3x = 12), divide both sides by 3 to solve for (x). In cases where the variable is divided, such as ( rac{x}{5} = 10), multiply both sides by 5. When negative numbers are involved, as in ( rac{-4w}{3} = -8), multiply both sides by 3 to eliminate the denominator, then divide by -4. Always check your solution by substituting it back into the original equation to ensure accuracy. Regular practice with various examples will enhance your proficiency in solving such equations effectively.
4.2 Solving Equations with Addition and Subtraction

Solving equations with addition and subtraction is a foundational skill in algebra. These equations typically involve isolating the variable by performing inverse operations. For example, in the equation (x + 7 = 15), subtract 7 from both sides to find (x = 8). Similarly, in (y ౼ 4 = 9), add 4 to both sides to determine (y = 13). It’s crucial to maintain balance by applying the same operation to both sides. When negative numbers are involved, such as (a ౼ 3 = -2), add 3 to both sides to solve for (a = 1). Always verify your solution by substituting it back into the original equation to confirm its validity. Regular practice will help build confidence in solving these types of equations efficiently.
4.3 Mixed Operations in Two-Step Equations
Mixed operations in two-step equations involve combining addition, subtraction, multiplication, and division. For example, solve 3(x — 4) + 2 = 20. First, distribute the 3: 3x, 12 + 2 = 20. Combine like terms: 3x ౼ 10 = 20. Add 10 to both sides: 3x = 30. Divide by 3: x = 10. Always check your solution by substituting it back into the original equation to ensure accuracy. Practice with various combinations to build proficiency in handling different sequences of operations. This skill enhances problem-solving abilities in algebra and real-world applications. Regular practice helps in mastering these equations efficiently and confidently.

Common Challenges and Mistakes
Students often struggle with incorrect operation order or forgetting to apply operations to both sides. Careless arithmetic errors and misapplying inverse operations are frequent pitfalls.
5.1 Identifying and Correcting Mistakes in Two-Step Equations
Identifying and correcting mistakes in two-step equations requires careful attention to detail. Common errors include mishandling negative signs, misapplying the order of operations, or incorrectly reversing steps. For example, students might divide before adding or subtracting, leading to incorrect solutions. To correct these mistakes, review each step systematically. Check if operations are applied in the reverse order of operations (PEMDAS) and ensure equality is maintained by performing the same operation on both sides. Additionally, plugging the solution back into the original equation can help verify accuracy. Regular practice with worksheets or online tools can build proficiency and reduce errors over time.
5.2 Avoiding Common Errors in Algebraic Manipulation
Avoiding common errors in algebraic manipulation is crucial for solving two-step equations accurately. One of the most frequent mistakes is mishandling negative signs, especially when distributing or moving terms. Another error is misapplying the order of operations, leading to incorrect simplification. Students often forget to apply operations to both sides of the equation, disrupting its balance. To prevent these errors, it’s essential to work step-by-step, double-checking each operation. Using inverse operations correctly and maintaining equality by performing the same action on both sides is vital. Regular practice and immediate feedback can help build awareness and reduce these mistakes, fostering stronger algebraic manipulation skills over time.

Real-World Applications of Two-Step Equations

Two-step equations are essential in real-life scenarios, such as calculating distances, budgeting expenses, and solving scientific formulas. They help model everyday problems involving multiple operations, making math practical and accessible for real-world challenges.
6.1 Solving Word Problems Using Two-Step Equations
Solving word problems using two-step equations involves translating real-life scenarios into mathematical expressions. These problems often require combining operations like multiplication and addition or division and subtraction. For example, calculating the total cost of items after applying a discount and adding tax, or determining the distance traveled when speeds and times vary. By identifying the unknown variable and applying the reverse order of operations, students can isolate the variable and find the solution. Word problems enhance critical thinking and practical application of algebraic concepts. They provide meaningful contexts for practicing two-step equations, making math more engaging and relevant to everyday life.
6.2 Practical Examples in Finance, Science, and Geometry
In finance, two-step equations can calculate interest rates or investment returns. For instance, determining the principal amount after adding compound interest. In science, they model phenomena like temperature changes over time or population growth; Geometry applies two-step equations to find missing dimensions, such as calculating the height of a triangle when the area and base are known. These real-world applications demonstrate how two-step equations are essential tools for problem-solving across various disciplines. By practicing these practical examples, students develop a deeper understanding of algebraic concepts and their relevance to everyday situations.

Resources for Learning and Practicing
Explore free worksheets, online tools, and educational videos for mastering two-step equations. Utilize textbooks and interactive apps to enhance your problem-solving skills and understanding of algebraic concepts.

7.1 Free Worksheets for Two-Step Equations (PDF Format)
Access a wide range of free PDF worksheets tailored for practicing two-step equations. These resources are designed to help students grasp algebraic concepts through structured exercises. Many worksheets include a variety of problems, such as solving equations with combined operations, word problems, and graphical interpretations. They are ideal for classroom use or self-study. Websites like Khan Academy, MathWorks, and Teachers Pay Teachers offer downloadable PDFs with answers included for easy grading. Some worksheets also feature interactive elements, allowing students to input their solutions digitally. These materials cater to different skill levels, ensuring learners can progress from basic to advanced problems seamlessly.
7.2 Online Tools and Calculators for Solving Two-Step Equations
Enhance your learning experience with online tools and calculators designed to solve two-step equations. Websites like Symbolab and Wolfram Alpha provide step-by-step solutions, breaking down complex problems into manageable parts. These platforms are perfect for verifying answers and understanding the problem-solving process. Additionally, interactive tools like IXL and Mathway offer practice exercises and video tutorials. Many of these resources are free and accessible, catering to students of all skill levels. Some tools also allow users to input equations and receive instant solutions, making them ideal for quick checks. These online resources complement traditional learning methods, offering a dynamic way to master two-step equations and improve algebraic skills effectively.
7.3 Recommended Textbooks and Study Guides
For in-depth learning, several textbooks and study guides are highly recommended for mastering two-step equations. Titles like “Elementary and Intermediate Algebra” by Harold R. Jacobs and “Algebra for College Students” by Robert F. Blitzer offer comprehensive coverage of two-step equations. These textbooks include detailed explanations, practice problems, and real-world applications. Additionally, study guides such as “Saxon Math” and “Holt McDougal Algebra” provide structured lessons and interactive exercises. Many of these resources are available in PDF format online, making them easily accessible. They cater to different learning styles and are ideal for students seeking to build a strong foundation in algebra and problem-solving skills.
Mastering two-step equations is a fundamental skill in algebra, enhancing problem-solving abilities and building a strong mathematical foundation. Keep practicing to achieve proficiency and confidence.
8.1 Summary of Key Concepts
In solving two-step equations, the essential steps include identifying the operations applied to the variable, applying the reverse order of operations, and simplifying both sides. Always perform inverse operations to isolate the variable, ensuring balance by applying the same operation to both sides. Simplify expressions by combining like terms and eliminating parentheses. Real-world applications highlight the practicality of these equations in finance, science, and everyday problem-solving. Regular practice with worksheets and online tools enhances mastery. Remember, consistency and attention to detail are crucial for accuracy. By following these principles, learners can confidently solve two-step equations and apply them effectively in various scenarios.
8.2 Encouragement to Continue Practicing
Mastery of two-step equations is achievable with consistent practice and dedication. Embrace challenges as opportunities to grow, and celebrate small victories along the way. Utilize free worksheets and online tools to reinforce your skills in a variety of problem types. Setting realistic goals and tracking progress can help maintain motivation. Surround yourself with resources like study guides or online communities to stay engaged. Remember, proficiency in algebra is a valuable skill that opens doors to advanced mathematics and real-world problem-solving. Keep pushing forward, and your confidence and speed will improve with time. The effort you invest now will lay a strong foundation for future success in mathematics.